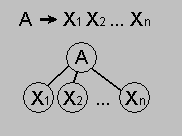
1. Формальные
языки
2. Формальные
грамматики
3. Классификация грамматик Хомского
4. КС-грамматики
5. КС-грамматика для арифметических
выражений
6. Форма Бекуса-Наура (БНФ)
7. Процедура компиляции
8. Грамматический разбор для
КС-грамматик методом "сверху-вниз"
9. Структурное представление входа
10. Грамматический разбор для
КС-грамматик методом "снизу-вверх"
11. Генерация кода для арифметического
выражения по его семантическому дереву
12. Генерация кода для операторов
13. Регулярные грамматики
Алфавит - линейно
упорядоченный набор некоторых вещей, называемых знаками.
Литера - синоним знака.
Предполагается, что есть способ их получения в
любом количестве экземпляров.
Символ - знак, имеющий определённый
общепринятый смысл, например "+". Заметим,
что этот термин также часто используют вместо
термина "литера".
Строка - конечная
последовательность знаков некоторого алфавита.
Длина строки -
количество символов в строке. Введём понятие строки
нулевой длины - e.
Алфавиты и строки принято обозначать греческими буквами, соответственно прописными и строчными.
d = a b g - d это результат сцепления строк a, b и g. Причём, a - префикс строки d, g - суффикс строки d, b - подстрока d.
S* - множество строк над алфавитом S.
S+ = S* / {e}.
Пример. S = {0, 1}. S* = {e, 0, 1, 00, 01, 10, ... }. S+ = {0, 1, 00, 01, 10, ... }.
Формальный язык над алфавитом S - некоторое подмножество множества S*. Так как формальные языки это множества, то к ним применимы все результаты теории множеств. Пример. L = L1 И L2 - L1 объединение языков L1 и L2.
Формальная грамматика - это
система правил, которая позволяет порождать
правильные строки языка
G = { T, N, S, P }, где T - множество символов
определяемого языка (их называют терминальными),
N - множество символов, которые используются лишь
для порождения языка (их называют нетерминальными),
S - начальный символ грамматики, P -
множество правил вывода вида a -> b. Кроме
того, должны выполняться следующие соотношения: T
З N = Ж, S О
N, a О (T И N)+, b О (T И N)*.
Пример: "Грамматика подмножества русского языка" .
T = { человек, собака, бежит, кусает },
N = {<предложение>, <подлежащее>,
<сказуемое>, <существительное>, <глагол>
},
S = <предложение>,
P = {
1) <предложение> ->
<подлежащее><сказуемое>,
2) <подлежащее> ->
<существительное>,
3) <сказуемое> -> <глагол>,
4) <существительное> -> человек,
5) <существительное> -> собака,
6) <глагол> -> бежит,
7) <глагол> -> кусает }.
В примере под символом понимается целое слово, причём нетерминальные символы заключены в угловые скобки. Эти общепринятые соглашения позволяют определять грамматику более компактно простым перечислением правил вывода (их называют также продукциями). Кроме того, этот способ позволяет дать попутно семантику нетерминальных символов. В более формальных построениях для обозначения терминальных символов принято использовать строчные буквы латинского алфавита, а для нетерминальных - прописные.
Пример более формальной записи грамматики: A -> BC, B -> D, C -> E, D -> a | b, D -> c | d. Здесь "|" - символ альтернативы. Его применение позволяет объединить запись правил с одинаковой левой частью.
Пример порождения строки языка с помощью
продукций грамматики (в скобках указаны номера
применяемых продукций):
<предложение> (1),
<подлежащее> <сказуемое> (2),
<существительное> <сказуемое> (4),
человек <сказуемое> (3),
человек <глагол> (6),
человек бежит.
Говорят, что "a непосредственно
порождает b", если к a можно применить такую подстановку,
что в результате получится b. Также
говорят, что "b непосредственно
сводится к a". Эту
операцию принято обозначать так: a Ю
b . Последовательность порождений a Ю b Ю g Ю ... Ю w кратко обозначают как a *Ю w и говорят "a порождает w"
или "w сводится к a". Примеры:
человек <сказуемое> Ю человек
<глагол>,
<предложение> *Ю человек бежит.
Сентенциальная форма -
произвольная строка, сводимая к начальному
символу грамматики.
Сентенция - сентенциальная форма, состоящая из одних терминальных символов.
Формальный язык, порождаемый грамматикой G - множество всех сентенций грамматики G. Обозначение - L(G).
Хомский по степени ограничений, накладываемых
на правила вывода, определил четыре класса
грамматик:
0 - Грамматики общего вида: нет
ограничений;
1 - Контекстно-зависимые (КЗ)
грамматики: a A b -> a p b, p <> e;
2 - Контекстно-свободные (КС)
грамматики: A -> a;
3 - Грамматики с конечным
числом состояний или регулярные
грамматики: A -> a, A -> aB.
Большинство современных языков программирования тяготеет к классу 2. Определения, которые здесь введены для грамматик, относят и к языкам, ими порождаемым.
Дерево грамматического разбора или дерево вывода позволяет в наглядной форме представить процесс порождения сентенциальной формы из начального символа грамматики. Эта возможность вытекает из следующей графической интерпретации правила КС-грамматики:
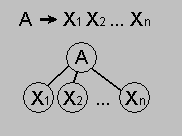
Пример дерева вывода сентенции aabb для грамматики 1) S -> AB, 2) A -> aA, 3) A -> a, 4) B -> bB, 5) B -> b:
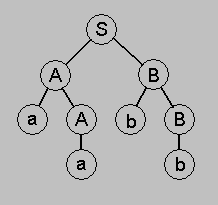
Пусть a *Ю b. Тогда грамматическим разбором b относительно a называется последовательность продукций, которые сводят b к a. Примеры: [5,4,3,2,1] - грамматический разбор aabb относительно S, [3,2,5,4,1] - ещё один такой разбор. В примерах продукции представлены своими номерами.
Связка - сводимая часть сентенциальной формы. Пример: в сентенциальной форме aAbb её подстрока a есть связка, так как есть правило A -> a, которое позволяет непосредственно свести aAbb к AAbb. Пример обозначения связки в сентенциальной форме: <a>Abb.
Грамматический разбор называется каноническим, если на каждом шаге для непосредственного сведения используется самая левая связка. В примере выше разбор [3,2,5,4,1] является каноническим.
Схема вывода - последовательность продукций, противоположная грамматическому разбору. Примеры: [1,2,3,4,5], [1,4,5,2,3].
Схема вывода называется левосторонней, если на каждом шаге непосредственного порождения в сентенциальной форме раскрывается самый левый нетерминальный символ. Пример левосторонней схемы вывода: [1,2,3,4,5].
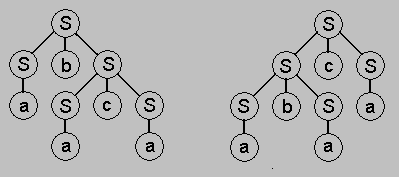
КС-грамматика называется однозначной, если все возможные схемы вывода любой её сентенциальной формы соответствуют одному и тому же дереву вывода. Пример неоднозначной грамматики: 1) S -> S b S, 2) S -> S c S, 3) S -> a . Для сентенции abaca возможны две схемы вывода, которым соответствуют разные деревья вывода:
| S S b S a b S a b S c S a b a c S a b a c a |
S S c S S b S c S a b S c S a b a c S a b a c a |
1) Z -> +E | -E | E,
2) E -> T + E | T - E | T,
3) T -> F * T | F / T | F,
4) F -> I | ( Z ),
5) I -> a | b | c | d.
Обозначения: Z - выражение, E - выражение без знака,
T - терм, F - фактор, I - идентификатор. Дерево
вывода для выражения ( a+b)*c:
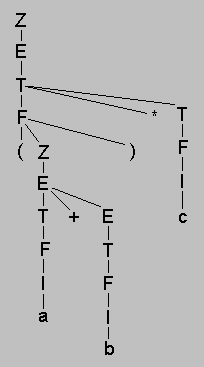
Правило вывода называется рекурсивным, если в правую его часть входит символ из его левой части. Рекурсивные правила приводят к циклам порождения, что в конечном итоге позволяет определять бесконечные языки с помощью конечного числа правил. Такая рекурсия называется прямой, в отличии от косвенной, при которой цикл порождения образуют несколько правил. Так, в предыдущем примере вместо E можно подставить T, вместо T - F, вместо F - ( E ), и т. д. - цикл замкнулся.
Кроме того, используются
понятия левосторонней и правосторонней
прямой рекурсии. В первом случае символ из левой
части правила находится в начале его правой
части. Во втором - в конце. В предыдущем примере
присутствует правосторонняя рекурсия. Доказано,
что грамматику всегда можно преобразовать таким
образом, что левосторонняя рекурсия будет
заменена правосторонней и наоборот. Преобразуем
грамматику предыдущего примера так, чтобы
избавиться от правосторонней рекурсии. Для этого
достаточно переписать два правила:
2) E -> E - T | E -T | T,
3) T -> T * F | T / F | F.
Предназначена для
формального определения синтаксиса языков
программирования и представляет собой
своеобразную форму записи грамматики языка.
Впервые была применена при создании языка
программирования Algol-60. Для определения языка
используется метаязык, который включает
следующие конструкции:
<Текст на естественном языке> - общие понятия
(нетерминальный символ);
Текст - конструкция определяемого языка
(терминальный символ);
| - символ альтернативы;
::= - "это есть" (вместо символа ->).
Пример:
<Программа> ::= <Составной оператор>
,
<Составной оператор> ::= begin <Конец
составного> ,
<Конец составного> ::= <Оператор> end
| <Оператор> ; <Конец составного> ,
. . .
<Оператор if> ::= if <Логическое
выражение> then <Оператор> else
<Оператор>,
. . .
Компиляция - процедура перевода программы с языка высокого уровня на язык нижнего уровня. Традиционно компиляция включает три основные фазы - лексический анализ, грамматический разбор (синтаксический анализ) и генерацию кода.
Лексический анализ - это первая фаза компиляции, в ходе которой распознаются так называемые лексемы. Реализуется программным модулем, который называется лексическим анализатором или сканером. Лексема - это последовательность литер, правила построения которой могут быть заданы регулярной грамматикой. Традиционно к лексемам относят идентификаторы (n), ключевые слова (k), константы (c) и служебные слова или разделители (c). Сканер преобразует строковое представление программы в последовательность более крупных структурных элементов, что в конечном итоге призвано уменьшить сложность решения общей задачи грамматического разбора программы. Рассмотрим пример входа и соответствующего выхода сканера, которые определены в терминах языка Prolog. Вход: "if sem > 0 then sem := sem - 1". Выход: [k("if"), n("sem"), s(">"), c("0"), k("then"), n("sem"), s(":="), n("sem"), s("-"), c("1")]. В реальных системах аргументы в скобках заменяют индексами элементов таблиц сканера, в которых "оседает" информация, не имеющая отношения к структуре программы, хотя и необходимая для последующих фаз компиляции. В сиcтеме Turbo Prolog легко построить сканер на основе стандартного предиката fronttoken(S,T,R). Этот предикат находит в строке S первую лексему T и формирует остаток строки R. При этом следует отметить, что лексема здесь понимается в смысле языка Turbo Prolog.
Грамматический разбор - фаза компиляции, которая преобразует программу в форме последовательности лексем в структурное представление, которое выражает структуру программы в наиболее явной форме.
Генерация кода - фаза компилятора, в ходе которой по структурному представлению программы строится её код на машинном языке.
Рассмотрим достаточно общий пример продукции КС-грамматики, например A -> B C D. Мы можем утверждать, что некоторая сентенция, которую будем впредь называть входом процедуры граматического разбора, суть правильная конструкция типа A, если начальная часть входа содержит конструкцию типа B, начальная часть остатка содержит конструкцию типа C, и т. д. Полагая, что вход задан списком лексем, мы можем выразить эту же мысль с помощью предиката parse(T, L, R) - "Вход L за вычетом остатка R содержит грамматическую конструкцию типа T". Для этого достаточно записать правило языка Prolog:
parse(a,La,Lr) :- parse(b,La,Lb), parse(c,Lb,Lc), parse(d,Lc,Lr).
Здесь типы конструкций заданы атомами a, b, c и d. Далее, если таким же образом выразить все продукции заданной грамматики, то мы получим Prolog-программу грамматического разбора и, желая, например, установить, что вход L содержит грамматическую конструкцию типа a, мы просто зададим цель parse(a, L, []).
Пример:
1) E -> T + E,
2) E -> T,
3) T -> F * T,
4) T -> F,
5) F -> id,
6) F -> ( E ).
Реализация правил грамматики
parse(expr,La,Lr) :- parse(term,La,Lb), parse(plus,Lb,Lc), parse(expr,Lc,Lr). parse(expr,La,Lr) :- parse(term,La,Lr). parse(term,La,Lr) :- parse(fact,La,Lb), parse(mul,Lb,Lc), parse(term,Lc,Lr). parse(term,La,Lr) :- parse(fact,La,Lr). parse(fact,La,Lr) :- parse(id,La,Lr). parse(fact,La,Lr) :- parse(bro,La,Lb), parse(expr,Lb,Lc), parse(brc, Lc,Lr).
Правила для терминальных символов
parse(id,[n(_)|Lr],Lr).
parse(plus,[s("+")|Lr],Lr).
parse(mul,[s("*")|Lr],Lr).
parse(bro,[s("(")|Lr],Lr).
parse(brc,[s(")")|Lr],Lr).
Этот метод является универсальным для КС-грамматик при условии отсутствия левосторонней рекурсии.
Предыдущая программа грамматического разбора устанавливает лишь правильность входа и не даёт его структурного представления, что безусловно необходимо для решения задачи компиляции. Одна из форм структурного представления - это семантическое дерево. Для арифметического выражения семантическое дерево может иметь следующую структуру:
tsemt = e(string, tsemt, tsemt); n(string)
Смысл аргументов структур e/3 и n/1 должен быть понятен из примера:
"a + b * (c - d)"
e("+", n("a"), e("*", n("b"), e("-",c,d))) .
Отметим, что для простоты мы пока не предусматриваем использование унарных арифметических операций и констант.
Введём в предикат parse четвёртый аргумент, который будет представлять семантическое дерево синтаксической конструкции, тип которой указан первым аргументом. Тогда правило для реализации, например , продукции E -> T + E будет иметь вид:
parse(expr,La,Lr,T) :- parse(term,La,Lb,Tt),
parse(plus,Lb,Lc),
parse(expr,Lc,Lr,Tt,T).
В правую часть этого правила мы были вынуждены включить вызов нового предиката parse/5 с пятью аргументами. Первые три его аргумента имеют точно такой же смысл как в предикате parse/4. Четвёртый аргумент - это семантическое дерево, которое соответствует части выражения предшествующей знаку "+", а пятый аргумент, как и в предикате parse/4, возвращает семантическое дерево всего выражения, в состав которого естественным образом должно быть включено поддерево, переданное в четвёртом аргументе. Задачу этого включения мы должны решить при составлении процедуры для предиката parse/5:
parse(expr,La,Lr,Tp,T) :- parse(term,La,Lb,Tt),
parse(plus,Lb,Lc),
parse(expr,Lc,Lr,e("+",Tp,Tt),T).
parse(expr,La,Lr,Tp,e("+",Tp,Tt)) :- parse(term,La,Lr,Tt).
Второе правило учитывает случай, когда за очередным термом не окажется знака "+".
Теперь мы можем полностью записать программу, которая по ходу грамматического разбора входа строит его структурное представление.
% Parser.pro - Нисходящий грамматический разбор арифметических выражений
include "Scaner.pro"
domains
tsemt = e(string,tsemt,tsemt); n(string)
predicates
parse(symbol,lstclex,lstclex,tsemt)
parse(symbol,lstclex,lstclex)
parse(symbol,lstclex,lstclex,tsemt,tsemt)
mktree(integer,tsemt)
tab(integer)
clauses
parse(expr,La,Lr,T) :- parse(term,La,Lb,Tt),
parse(plus,Lb,Lc),
parse(expr,Lc,Lr,Tt,T).
parse(expr,La,Lr,T) :- parse(term,La,Lr,T).
parse(term,La,Lr,T) :- parse(fact,La,Lb,Tf),
parse(mul,Lb,Lc),
parse(term,Lc,Lr,Tf,T).
parse(term,La,Lr,T) :- parse(fact,La,Lr,T).
parse(fact,La,Lr,T) :- parse(id,La,Lr,T).
parse(fact,La,Lr,T) :- parse(bro,La,Lb),
parse(expr,Lb,Lc,T),
parse(brc,Lc,Lr).
parse(id,[n(Name)|Lr],Lr,n(Name)).
parse(plus,[s("+")|Lr],Lr).
parse(mul,[s("*")|Lr],Lr).
parse(bro,[s("(")|Lr],Lr).
parse(brc,[s(")")|Lr],Lr).
parse(expr,La,Lr,Tp,T) :- parse(term,La,Lb,Tt),
parse(plus,Lb,Lc),
parse(expr,Lc,Lr,e("+",Tp,Tt),T).
parse(expr,La,Lr,Tp,e("+",Tp,Tt)) :- parse(term,La,Lr,Tt).
parse(term,La,Lr,Tp,T) :- parse(fact,La,Lb,Tf),
parse(mul,Lb,Lc),
parse(term,Lc,Lr,e("*",Tp,Tf),T).
parse(term,La,Lr,Tp,e("*",Tp,Tf)) :- parse(fact,La,Lr,Tf).
%----- Предикаты для рисования дерева -----
tab(0) :- !.
tab(N) :- write(" "),M=N-1,tab(M).
mktree(Lev,n(N)) :- tab(Lev),write(N),nl.
mktree(Lev,e(I,L,R)) :-
NLev=Lev+3,
mktree(Nlev,R),
tab(Lev),Write(I),nl,
mktree(NLev,L).
%------------------------------------------
goal
makewindow(1,10,7,"Tree",0,0,25,80),
S="(a+b)+(c+d)", write(S), nl,
scaner(S,L), write(L), nl,nl,
parse(expr,L,[],T), write(T), nl,nl,
mktree(0,T),
readchar(_),
removewindow.
Выходные данные программы Parser.pro:
(a+b)+(c+d)
[s("("),n("a"),s("+"),n("b"),s(")"),s("+"),s("("),n("c"),s("+"),n("d"),s(")")]
e("+",e("+",n("a"),n("b")),e("+",n("c"),n("d")))
d
+
c
+
b
+
a
Мы полагаем, что модуль Scaner.pro, включаемый в эту программу, реализует предикат scaner/2, выполняющий лексический анализ входа. Приведённую программу не трудно обобщить на случай арифметических выражений общего вида.
По сути нисходящий грамматический разбор основан на процедуре перебора сентенций, которые генерируются по правилам грамматики. Разбор начинается с начального символа грамматики, то есть сначала отыскивается правило с начальным символом грамматики в левой части. Далее с помощью соответствующего правила раскрывается первый нетерминальный символ правой части этого правила и так далее. Рано или поздно этот процесс приведёт к порождению терминального символа. Последний сравнивается с очередным символом входа и в случае совпадения процес продолжается для очередного нетерминального символа последнего вступившего в действие правила. В противном случае происходит возврат с заменой некоторого правила другим с такой же левой частью.
Возможна и другая логика процесса порождения - восходящая. Про восходяший грамматический разбор говорят, что он направляется входной строкой. Для очередного символа входа отыскивается правило, правая часть которого начинается с этого символа. Следующий нетерминальный символ этого правила рассматривается как временная цель, к которой должен стремиться разбор. Когда последовательно будут достигнуты все цели, определяемые правой частью правила, нетерминальный символ его левой части может быть использован для вовлечения в разбор следующего правила и так далее, если, конечно, этот символ сам не является целью разбора.
Рассмотрим пример построения процедуры
восходящего грамматического разбора. Так как для
этого метода не имеет значения вид рекурсии, то
для разнообразия возьмём грамматику с
левосторонней рекурсией:
E -> E + T | T,
T -> T * F | F,
F -> ( E ) | id.
Предикат для восходящего разбора имеет следующую реляционную схему
parse( Input, Rest, F, TF, Z, TZ ),
где F - тип синтаксической конструкции, предшествующей входу Input; Z - тип целевой конструкции, начинающейся с F и продолжающейся в начальной части входа Input за исключением остатка Rest. TF и TZ - семантические деревья конструкций F и Z.
Далее приведена процедура для определения предиката parse. В процедуре используется понятие пустой синтаксической конструкции ng, которой соответствует пустое семантическое дерево nil. Она обозначает фиктивное начало синтаксической конструкции. Кроме того, в приведённой процедуре более широко используются возможности языка Prolog, чем в примере предыдущего раздела. Следует обратить внимание также на то, что в этом случае порядок разбора совпадает с порядком построения семантического дерева.
parse(La,La,Z,Tz,Z,Tz).
parse([n(S)|La],Lr,ng,nil,Z,Tz) :- parse(La,Lr,fact,n(S),Z,Tz).
parse([s("+")|La],Lr,expr,Te,Z,Tz) :-
parse(La,Lb,ng,nil,term,Tt),
parse(Lb,Lr,expr,e("+",Te,Tt),Z,Tz).
parse(La,Lr,term,T,Z,Tz) :- parse(La,Lr,expr,T,Z,Tz).
parse([s("*")|La],Lr,term,Tt,Z,Tz) :-
parse(La,Lb,ng,nil,fact,Tf),
parse(Lb,Lr,term,e("*",Tt,Tf),Z,Tz).
parse(La,Lr,fact,T,Z,Tz) :- parse(La,Lr,term,T,Z,Tz).
parse([s("(")|La],Lr,ng,nil,Z,Tz) :-
parse(La,[s(")")|Lb],ng,nil,expr,T),
parse(Lb,Lr,fact,T,Z,Tz).
goal
scaner("(a+b)*c",L),
parse(L,[],ng,nil,expr,T), write(T),nl.
Выход программы:
e("*",e("+",n("a"),n("b")),n("c"))
Сначала определим архитектуру ЦВМ, для которой предполагается строить код. Пусть это будет учебная машина, которая подробно изучалась в предшествующих курсах.
Далее мы определим предикат gencode(E), функция которого состоит в преобразовании семантического дерева арифметического выражения, заданного аргументом, в соответствующий код. Будем считать, что код выводится как побочный результат выполнения предиката gencode в текстовом виде на языке ассемблера. Язык ассемблера, как форму представления кода, мы выбираем для наглядности, полагая, что задача необходимого в этом случае преобразования ассемблерного кода в бинарный код менее принципиальна.
В отношении кода, который строит предикат gencode, мы примем одно важное допущение - будем считать, что код для арифметического выражения строится таким образом, что его выполнение должно приводить к формированию результата в аккумуляторе.
Последнее предположение позволяет сразу же решить задачу для частного случая, когда семантическое дерево содержит один терминальный элемент, соответствующий выражению-переменной:
gencode(n(Name)) :- write(" lda ", Name), nl.
В общем случае, когда корнем семантического дерева является узловой элемент, соответствующий арифметической операции, мы воспользуемся рекурсией:
gencode(e(Instr,Tl,Tr)) :-
gencode(Tr),
write{" sta _m"), nl,
gencode(Tl),
toMnem(Instr, Mnem),
write(" ", Mnem, " _m), nl.
Здесь предикат toMnem преобразует арифметичекую операцию в соответствующее её мнемоническое обозначение на ассемблере. Однако, в данном правиле есть один очень существенный изъян - одна и та же рабочая переменная _m используется на разных уровнях рекурсии, что приводит к генерации неправильной программы. Для устранения этого недостатка необходимо модифицировать имя рабочей переменной в зависимости от уровня рекурсии. Для этого в число аргументов предиката gencode включим номер текущего уровня рекурсии. Окончательно получим следующую процедуру для определения предиката gencode/2.
gencode(n(Name), _) :- write(" lda ",Name), nl.
gencode(e(Instr,Tl,Tr), Lev) :-
NewLev = Lev + 1,
gencode(Tr, NewLev),
write{" sta _m",Lev), nl,
gencode(Tl, NewLev),
toMnem(Instr,Mnem),
write(" ", Mnem, " _m",Lev), nl.
Пример. Цель ?- gencode(e("+", e("*", n("a"), n("b")), n("c")), 0) приведёт с генерации следующего кода.
lda c
sta _m0
lda b
sta _m1
lda a
mul _m1
add _m0
Для архитектуры ЦВМ со стеком генерация кода для арифметических выражений может быть существенно упрощена, если для размещения рабочих переменных, хранящих промежуточные результаты вычислений, использовать стек. В этом случае вместо команды sta мы должны сгенерировать команду помещения значения аккумулятора в стек. Так как порядок формирования рабочих переменных соответствует дисциплине стека, то в соответсвующий момент нужное значение окажется в вершине стека - остаётся лишь воспользоваться им и не забыть вытолкнуть из стека.
Пример генерации кода, который мы рассмотрели выше, показывает, что качество полученного кода далеко от идеала. Это следствие простоты алгоритма, по которому он строится. Приведем комплекс более сложных правил, которые приводят к более гибкой схеме генерации. Правила приведены для операции сложения и легко могут быть распространены на общий случай. Следует отметить, что для некоммутативных операций (-, /) возможности улучшения кода несколько хуже.
gencode(e("+",n(A),n(B)), _) :- !,
write(" lda ", A), nl,
write(" add ", B), nl.
gencode(e("+",Tl,n(B)), Lev) :- !,
gencode(Tl, Lev),
write(" add ", B), nl.
gencode(e("+",n(A),Tr), Lev) :- !,
gencode(Tr, Lev),
write(" add ", A), nl.
gencode(e("+",Tl,Tr), Lev) :-
NewLev = Lev + 1,
gencode(Tr, NewLev),
write(" sta _m", Lev), nl,
gencode(Tl, NewLev),
write(" add _m", Lev), nl.
Генерация кода для операторов основана на использовании стандартных схем построения кода, которые принято называть шаблонами.
Для примера рассмотрим генерацию кода для оператора if. Сначала надо установить форму семантического дерева для этого оператора. Синтаксису "if <Логическое выражение> then <Оператор> else <Оператор>" хорошо соответствует следующая форма бинарного семантического дерева:
e("if", Tl, e("fi", Tt, Te)) .
Здесь Tl, Tt и Te - соответсвенно семантические деревья для логического выражения, оператора после then и оператора после else. Эта форма может быть применена и для сокращённой формы оператора if с отсутствующей else-частью. Для этого достаточно ввести в рассмотрение пустое семантическое дерево, обозначим его nil, и положить Te = nil.
Далее определим правило для предиката gencode/2, в соответствии с которым будет генерироваться код для оператора if. Мы сохраним реляционную схему предиката gencode, полагая, что он должен сохранить способность генерации кода для арифметических выражений. Предварительно необходимо принять соглашение о той форме, в которой будет формироваться результат выполнения кода для логического выражения. Будем считать, что этот результат формируется в аккумуляторе и принимает значение 0, если логическое выражение истинно, и какое-нибудь другое значение в противном случае. Руководствуясь идеей шаблона мы получим.
gencode(e("if", Tl, e("fi", Tt, Te)), Lev) :-
gencode(Tl, Lev),
write(" comp _z"), nl,
write(" jeq _e"), nl,
gencode(Tt, Lev),
write(" j _fi"),
write("_e nop"), nl,
gencode(Te, Lev),
write("_fi nop"), nl.
Переменная _z с значением 0 должна быть определена в генерируемой программе где-нибудь в другом месте. Имена _e и _fi это метки операторов генерируемой программы, на которые передаётся управление. И с ними возникают некоторые проблемы. Если в генерируемой программе будет несколько операторов if, то необходимо обеспечить оригинальность их меток. Аргумент Lev в данном случае не может помочь, так как метки должны быть оригинальными по порядку появления операторов if в программе, а не по уровням рекурсии. Определим предикат, который формирует новый номер при очередном обращении к нему.
getcnt(Cnt) :- retract(cnt(Cnt),!,
NewCnt = Cnt + 1,
assert(cnt(NewCnt)).
getcnt(0) :- retractall(cnt(_)), assert(cnt(0)).
Теперь мы можем записать правило генерации кода для оператора if в окончательном виде.
gencode(e("if", Tl, e("fi", Tt, Te)), Lev) :-
getcnt(M),
gencode(Tl, Lev),
write(" comp _z"), nl,
write(" jeq _e", M), nl,
gencode(Tt, Lev),
write(" j _fi", M),
write("_e", M, " nop"), nl,
gencode(Te, Lev),
write("_fi", M, " nop"), nl.
Аналогичным образом мы можем поступить и для других операторов. Отметим некоторые особенности составного оператора. Его семантическое дерево целесообразно представить в такой форме.
e("co", T1, e("co", T2, e("co", ... e("co", Tn, nil)...)))
Здесь T1, T2, ..., Tn - семантические деревья операторов, составляющих оператор присваивания. Принятая организация семантического дерева для составного оператора приводит к следующему правилу генерации его кода.
gencode(nil, _) :- write(" nop"), nl.
gencode(e("co", T, Te), Lev) :-
gencode(T, Lev),
gencode(Te, Lev).
Слово регулярные указывает на наличие некой регулярности в сентенциях языка. Другое название для этих грамматик - грамматики с конечным числом состояний - указывает на то, что анализатор для распознавания правильных строк любого регулярного языка может быть построен на основе конечной памяти, даже для входа бесконечной длины. Для КС-грамматик это не так - в общем случае память должна быть бесконечной. И лишь некоторым утешением может служить тот факт, что для КС-грамматик память анализатора эффективно может быть построена по стековому принципу.
Для регулярных грамматик вводится понятие недетерминированного автомата, представляемого графом. Эта возможность вытекает из интерпретации правил регулярной грамматики дугами графа.
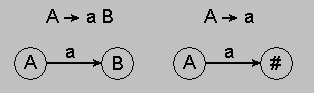
Пример. Недетерминированный автомат для грамматики: S -> a | aA, A -> a | aB, B -> b | bS .
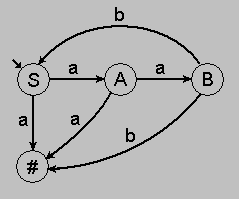
На недетерминированнность автомата указывает то, что из некоторых вершин его графа могут выходить дуги с одинаковыми ассоциированными терминальными символами. Смысл этой абстракции состоит в том, что если в графе недетерминированного автомата для некоторой входной строки существует путь, который ведёт из начальной вершины (отмечена короткой стрелкой) в конечную(обозначена знаком #), асоциированные символы дуг которого составляют входную строку, то данная строка является сентенцией языка, определяемого данной регулярной грамматикой. Для таких строк есть специальное название - строка воспринимаемая автоматом. Таким образом, с точки зрения недетерминированного автомата язык - это множество воспринимаемых им строк. Теоретически доказана эквивалентность понятий регулярной грамматики и недетерминированного автомата. Кроме того, также теоретически доказано, что любой недетерминированный автомат может быть преобразован в эквивалентный детерминированный автомат. Эквивалентность здесь понимается в смысле эквивалентности множеств строк, воспринимаемых обоими автоматами. Более того, существуют формальные процедуры для преобразования недетерминированного автомата в детерминированный. Мы, ограничиваясь в этом вопросе здравым смыслом, можем предложить такой детермининированный автомат для нашего примера.
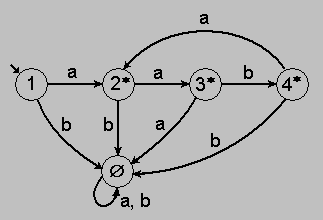
Вершины графа детерминированного автомата не имеют непосредственной связи с вершинами графа недетерминированного автомата и поэтому им даны совершенно другие обозначения. Любая входная строка должна считаться правильной, если она переводит автомат в состояние, отмеченное звёздочкой.
Важно отметить, что возможность построения детерминированного автомата, эквивалентного регулярной грамматике, открывает путь к реализации соответствующего распознавателя. Хотя, например, возможности языка Prolog позволяют непосредственно реализовать и недетерминированный автомат. Действительно, граф недетерминированного автомата можно представить следующей базой данных.
e('S', 'a', '#'). e('S', 'a', 'A'). e('A', 'a', '#').
e('A', 'a', 'B'). e('B', 'b', '#'). e('B', 'b', 'S').
Полагая, что вход автомата задан списком литер, определим предикат goodstr, который согласуется с базой данных для строк воспринимаемых автоматом. Первый аргумент этого предиката задаёт вход автомата, а второй - его начальное состояние.
goodstr([], '#'). goodstr([Ch|T], X) :- e(X, Ch, Y), goodstr(T, Y).
Пример. Для проверки строки aaba на воспринимаемость автоматом мы должны сформировать такую цель.
?- goodstr(['a','a','b','a'], 'S').
Предикат goodstr можно использовать и для генерации воспринимаемых автоматом строк. Однако, учитывая, что множество таких строк бесконечно, для корректного решения такой задачи определим предикат genstr, который генерирует все строки, воспринимаемые автоматом, длина которых не превышает заданную.
genstr(_, [], '#').
genstr(Len, [Ch|T], X) :- Len>0,
NewLen = Len - 1, e(X, Ch, Y), genstr(NewLen, T, Y).
Пример.
?- genstr(4, Str, 'S') Str = ['a'] Str = ['a','a'] Str = ['a','a','b'] Str = ['a','a','b','a']
Copyright г Барков Валерий Андреевич, 2001