1. Понятие об алгоритме
2. Пятиблочная машина фон Неймана
3. Языки программирования высокого
уровня
4. Язык схем алгоритмов (ЯСА)
5. Классификация пограмм
6. Структурное программирование
7. Исчисление высказываний
Алгоритм (Марков) - точное предписание определяющее процесс преобразования информации, ведущий от варьируемых исходных данных к искомому результату.
Алгоритм Евклида (3 в. до
н.э.) решения задачи нахождения общей меры двух
отрезков, длины которых выражаются натуральными
числами:
Шаг 1. Если отрезки равны, то длина любого отрезка
и есть искомый результат. Конец. Иначе перейти к
шагу 2.
Шаг 2. Больший отрезок замени отрезком, длина
которого равна разности длин отрезков. Перейти к
шагу 1.
Этот алгоритм более известен как алгоритм нахождения наибольшего общего делителя двух натуральных чисел.
Алгоритм Евклида - это первый алгоритм в истории человечества, сформулированный как научный результат. Само слово "алгоритм" происходит от имени арабского математика Мохаммеда ибн Муса Альхваризми, который в IX веке внёс значительный вклад в распространение существовавших тогда методов вычислений. В научной литературе вместо слова "алгоритм" иногда употребляют слово "алгорифм".
Свойства алгоритма
1. Пошаговость.
Предписание должно быть составлено таким
образом, чтобы определяемые им операции
выполнялись последовательно одна за другой.
2. Осуществимость. Предписание
должно быть составлено таким образом, чтобы его
исполнение было во всех деталях однозначно
осуществимо и не требовало никаких свободно
принимаемых решений.
3. Воспроизводимость. Одинаковые
исходные данные должны всегда приводить к одному
и тому же результату.
4. Замкнутость. Предписание должно
быть составлено таким образом, чтобы его
исполнение не требовало информации отличной от
входных данных и самого предписания.
5. Конечная память. Предписание
должно быть составлено таким образом, чтобы его
осуществление было возможно при ограниченном
объёме промежуточных результатов.
6. Конечное число шагов.
Предписание должно быть составлено таким
образом, чтобы его осуществление выполнялось за
конечное число шагов.
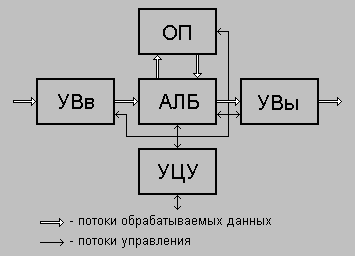
Устройство, которое способно выполнять алгоритмы будем называть интерпретатором. Исторически долгое время единственным интерпретатором алгоритмов был человек. В 1945 году фон Нейман определил принципы программного управления, которые вместе составили программный принцип решения задач. Его суть состоит в следующем. Человек заранее планирует ход вычислительного процесса решения задачи (алгоритм) и описывает его в виде последовательности элементарных инструкций, называемой программой решения задачи. Когда программа составлена, решение задачи становится чисто механическим делом и может быть "поручено" автомату. Автомат его выполнит точно по программе и, что особенно важно, значительно быстрее человека. Автомат для вычислений получил название цифровой вычислительной машины ( ЦВМ). Гипотетическая ЦВМ, в которой реализованы принципы программного управления, получила название пятиблочной машины фон Неймана (Рис. 1).
Рис. 1. Пятиблочная машина фон Неймана

Обозначения: АЛБ - арифметико-логический блок; ОП - основная память; УВв - устройство ввода; УВы - устройство вывода; УЦУ - устройство центрального управления, включая пульт управления.
ОП предназначена для хранения программы и обрабатываемых данных. Программа для ЦВМ представляет собой последовательность инструкций и может рассматриваться как специфический вид данных. В этой связи различают проблемные данные (данные решаемой задачи) и управляющие данные (инструкции программы). Инструкции ЦВМ имеют операционно-адресную структуру. Операционная часть содержит код выполняемой операции. Адресная часть указывает местоположение в ОП данных участвующих в операции - операндов.
УЦУ последовательно читает инструкции программы из ОП и побуждает другие блоки машины к их выполнению. АЛБ выполняет арифметические и логические операции над порциями данных из ОП и их результаты засылает снова в ОП. УВв и УВы предназначены для преобразования физического представления данных, вводимых в ОП и выводимых и неё.
В соответствие с назначением инструкции ЦВМ делят на типы - арифметико-логические, посылочные, ввода-вывода и управления. Посылочные инструкции служат для перемещения данных из одного места ОП в другое. Инструкции ввода-вывода приводят в действие соответствующие устройства и тогда происходит программно управляемая передача данных между внешней средой и ОП ЦВМ. Инструкции управления не изменяют проблемных данных и служат для изменения порядка выполнения инструкций программы.
Составление программ в машинных инструкциях - достаточно трудоёмкое занятие, требующее кропотливости и терпения. Оно доступно лишь программистам, подробно изучившим структуру машины и систему её команд. Для повышения производительности труда программиста были разработаны языки высокого уровня (ЯВУ) - Pascal, C++ и т.д. Программа на ЯВУ имеет вид текста с удобными символическими обозначениями инструкций и данных. Такой текст называют исходным модулем (ИМ) программы. Однако ЦВМ не может выполнить непосредственно программу в виде ИМ - её машинный язык отличается от ЯВУ. Проблема решается с помощью компилятора - специальной программы, которая переводит ИМ с ЯВУ на машинный язык. В результате получается исполняемый модуль (ИМ) программы на машинном языке, который может быть загружен в ОП ЦВМ и выполнен.
Программа на ЯВУ должны быть "понятна" компилятору. Для этого её надо писать по определённым правилам, которые принято называть синтаксисом ЯВУ. Синтаксически правильная программа переводится компилятором в ИМ. Если в программе есть синтаксические ошибки, то компилятор выведет сообщения о них. Синтаксические ошибки также называют ошибками периода компиляции. Могут ли быть ошибки в откомпилированной программе? Ответ - да. Такие ошибки называют семантическими (смысловыми) или ошибками периода выполнения. Классический пример - деление на нуль. Кроме этих двух видов ошибок не следует забывать и о самых главных - ошибках в алгоритме, которые называют алгоритмическими.
Задача программиста - писать программы без ошибок. Но это практически недостижимо. Поэтому возникает необходимость в тестировании и отладке программы. Тестирование - это контрольное выполнение программы с целью обнаружения ошибок в ней. Отладка - это определение местонахождения ошибки, выявленной в ходе тестирование, и её исправление. Было бы наивно считать, что тестирование доказывает правильность программы. Известно, что в современных сложных программных системах ошибки выявляются на протяжении всей их жизни. Гарантию отсутствия ошибок в программе может дать лишь способ доказательных рассуждений в ходе построения программы, подобно тому как доказываются теоремы в геометрии. Овладеть этим искусством достаточно сложно, но другого пути к построению безошибочных программ нет.
ЯСА прост, нагляден и для нас интересен тем, что позволяет сразу же приступить к изучению искусства программирования. Рассмотрим его конструкции.
1. Константы. Вводя такую конструкцию, мы просто констатируем тот факт, что в ЯСА разрешается использовать константы в их обычной математической форме записи. Пример: 1, -23.45.
2. Переменные. Переменной называется величина, которая в ходе выполнения программы может принимать различные значения. Математическое понятие переменной - это абстракция от текущего значения. С технической точки зрения переменной соответствует ячейка основной памяти ЦВМ, в которой записано её значение. Для ссылки на ячейку в машинной программе используют её адрес (номер ячейки в ОП), роль которого в ЯВУ играет имя переменной. В этой связи запись "x + y" имеет в программе следующий смысл: "содержимое ячейки с именем x сложи с содержимым ячейки с именем y". Имена переменных, которые мы используем при написании ИМ программы, компилятор заменит адресами соответствующих ячеек ОП, и, более того, он же эти номера сам и определит. В ЯСА переменным можно давать любые имена (в пределах разумного, естественно).
3. Арифметические операции. Это +, -, * и /.
4. Арифметические выражения. Арифметическое выражение (АВ) - это комбинация констант, переменных, знаков арифметических операций и круглых скобок, имеющая определённый математический смысл. Мы с программной точки зрения будем рассматривать запись АВ как инструкцию для вычисления его результата. Пример: пусть переменная a имеет значение 10, тогда выражение "a + 2" может рассматриваться как инструкция для машины, в результате выполнения которой будет получено в данном случае 12. Следует заметить, что константа и переменная - это частные случаи АВ.
5. Операторы присваивания. Оператор присваивания позволяет в программе выразить мысль о необходимости запомнить результат вычисления АВ в качестве значения заданной переменной. В ЯСА оператор присваивания имеет следующую структуру: <Имя переменной> ":=" <АВ>. Знак := это знак операции присваивания. В угловых скобках при описании ЯВУ принято записывать общие понятия, конкретные представители которых должны стоять на соответствующем месте. Наоборот, в кавычках записывают символы самого ЯСА, которые должны оказаться в программе, но уже без кавычек. Суть оператора присваивания можно выразить как инструкцию вычислить результат АВ справа от знака операции присваивания и запомнить его в качестве значения переменной, имя которой указано слева от знака операции присваивания. Таким образом оператор присваивания позволяет изменять состояние памяти программы, под которой понимается совокупное значение всех её переменных.
Пример. Задача: даны две переменные a и b. Какие операторы и в каком порядке надо выполнить, чтобы поменять местами значения этих переменных. Ответ: w := a; a := b; b := w . Как мы видим, понадобилась дополнительная переменная w, которая используется для временного хранения первоначального значения переменной a. Такие переменные называют рабочими.
6. Логические выражения.
Логическое выражение (ЛВ) имеет структуру:
<АВ> < "<" | "<=" | "=" |
"<>" | ">=" | ">" > <АВ> .
Здесь знак "|" - символ альтернативы. Он
показывает, что только один элемент надо взять из
числа тех, которые перечислены в угловых скобках.
В скобках же перечислены обычные знаки
сравнения. Запись логического выражения мы также
рассматриваем как инструкцию вычисления его
значения, в данном случае, логического -
"истина" или "ложь". Примеры: 1) 3 > 5 -
"ложь"; 2) a + 1 <> 4 - значение
этого ЛВ зависит от значения переменной a.
7. Блоки и стрелки. Блоки и стрелки используются для построения схемы алгоритма (СА), которая в наглядной графической форме позволяет проследить ход выполнения алгоритма . Форма записи и содержание блоков ЯСА показаны на рис. 2.
Рис. 2. Блоки ЯСА: а) Блок "НАЧАЛО"; б) Блок "КОНЕЦ"; в) Операторный блок; г) Логический блок; д) Блок ввода; е) Блок вывода; ж) Слияние стрелок; з) Размеры блоков.
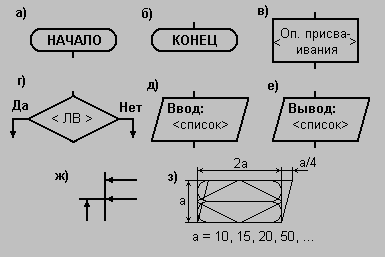
Блоки "НАЧАЛО" и "КОНЕЦ" определяют начало и конец вычислительного процесса. Операторный блок содержит один или несколько операторов присваивания. Он показывает, что в соответствующем месте вычислительного процесса должны быть выполнены его операторы присваивания в порядке их записи. Логический блок содержит ЛВ, которое рассматривается как условие перехода в СА. Если значение ЛВ "истина", то следующим выполняется блок по стрелке "Да". В противном случае - по стрелке "Нет". Логический блок привносит в ЯСА возможность выражения логических рассуждений и позволяет изменять ход вычислительного процесса в зависимости от значений обрабатываемых данных. Блоки ввода-вывода указывают на необходимость передачи данных между ОП и внешней средой. Список ввода может содержать только имена переменных. При выполнении блока ввода они все получают соответствующие входные значения. Список вывода может содержать арифметические выражения. При выполнении оператора вывода их значения выводятся из машины.
Рассмотрим некоторые свойства СА, которые формально позволяют судить об их правильности. Так как присвоить значение переменной можно только при выполнении оператора присваивания или в блоке ввода (как вводимое значение), то имя любой переменной в СА должно сначала встретиться в левой части одного из операторов присваивания или в списке ввода одного из блоков ввода. В противном случае говорят, что соответствующая переменная не инициализирована, и это значит, что обращение к её значению свидетельствует об ошибке в алгоритме.
Строго регламентировано количество выходных стрелок из блоков: из блока "КОНЕЦ" - ни одной, из логического блока - две, из остальных блоков - одна. Все блоки (кроме блока "НАЧАЛО") должны иметь по одной входной стрелке. Стрелки могут сливаться, но не могут расходиться. Это означает, что блок может получать управление после выполнения разных блоков, но никакие блоки не могут получить управление одновременно - все блоки СА выполняются строго последовательно.
Мы закончили определение ЯСА, и теперь можем рассмотреть пример его применения. На рис. 3 приведена запись алгоритма Евклида в терминах ЯСА.
Рис. 3. Схема алгоритма Евклида
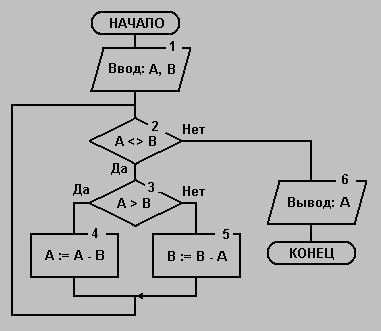
Проследим работу алгоритма для входа A = 9 и B = 6. Для этого составим так называемую трассировочную таблицу алгоритма:
| Номер блока | A | B | Значение ЛВ | Примечание |
| 1 | 9 | 6 | Ввод: A, B | |
| 2 | 9 | 6 | "истина" | Переход к бл. 3 |
| 3 | 9 | 6 | "истина" | Переход к бл. 4 |
| 4 | 3 | 6 | ||
| 2 | 3 | 6 | "истина" | Переход к бл. 3 |
| 3 | 3 | 6 | "ложь" | Переход к бл. 5 |
| 5 | 3 | 3 | ||
| 2 | 3 | 3 | "ложь" | Переход к бл. 6 |
| 6 | 3 | 3 | Вывод: A |
В таблице колонки "A" и "B" содержат значения соответствующих переменных, которые они принимают после выполнения очередного блока алгоритма, номер которого указан в колонке "Номер блока". В колонке "Значение ЛВ" указано значение ЛВ соответствующего логического блока, которое определяет номер следующего выполняемого блока. Очевидно, что алгоритм выведет значение 3 и остановится.
ЯСА даёт нам набор элементарных конструкций, которые мы можем использовать для разработки алгоритмов. Мы полностью должны отдавать себе отчёт в том, что в этот язык нельзя произвольно вносить какие-либо новые конструкции. В этой связи удобно представить, что ЯСА соответствует ЯСА-машина, которая является интерпретатором алгоритмов на ЯСА. В этом случае понятно, что мы не можем изменить язык записи алгоритмов без соответствующей переделки машины.
Так как программа - это выражение алгоритма в машинных терминах, то это позволяет нам называть СА для ЯСА-машины программой.
( Программы ( Линейные, С разветвлениями ( Нециклические, Циклические ) ).
Программа называется линейной, если в ней нет логических блоков. В линейной программе блоки выполняются строго в одном порядке независимо от значений входных данных. В программах с разветвлениями порядок выполнения блоков зависит от входных данных - некоторые блоки в некоторых реализациях программы могут вообще не выполняться. В нециклических программах ни один блок не может быть выполнен более одного раза. В циклических программах некоторые блоки могут выполняться многократно.
Алгоритм Евклида - циклический. Подавляющее большинство программ, имеющих практическое значение - циклические.
При создании программы мы связаны возможностями базового языка, на котором эта программа должна быть записана. Структурное программирование исходит из того, что первоначально мы можем формулировать программу в абстрактных понятиях, предполагая, что в принципе могут быть созданы машины для их интерпретации. Далее выполняется процесс детализации этой абстрактной программы на основе использования фиксированного числа базовых управляющих конструкций. В результате мы получим более детальную правильную программу, но выраженную ещё в абстрактных понятиях. Продолжая процесс детализации, мы должны в результате придти к программе, выраженной в терминах базового языка программирования.
Доказано, что для детализации абстрактной программы достаточно располагать управляющими конструкциями трёх видов (Рис. 4, а, б и в). Но для удобства выражения обычно в их число вводят и дополнительные конструкции (Рис. 4, г).
Рис. 4. Базовые конструкции структурного программирования: а) конструкция сочленения; б) конструкция выбора; в) конструкция "выполнять пока"; г) конструкция "повторять до"
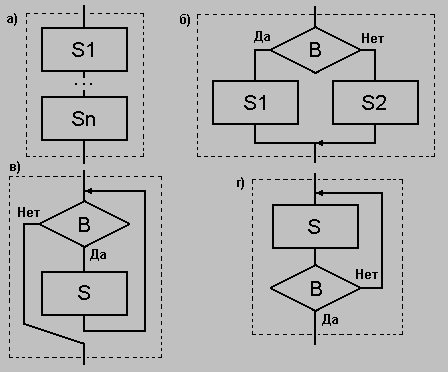
Рассмотрим базовые конструкции структурного программирования более подробно. Пунктирный контур вокруг каждой конструкции показывает, что она может служить для детализации одного операторного блока программы более высокого абстрактного уровня. В этой связи у каждой конструкции может быть только один вход и только один выход.
Конструкция сочленения выражает мысль о том, что некоторая сложная абстрактная операция может быть представлена как последовательность конечного числа более простых операций S1, S2, ..., Sn.
Конструкция выбора полезна в тех случаях, когда суть сложной абстрактной операции состоит в выборе одной из двух более простых операций S1 или S2 по условию. ЛВ B определяет условие выбора.
Следующие две конструкции циклические. Они позволяют выразить мысль о том, что некоторая сложная абстрактная операция может быть представлена как результат многократного повторения более простой операции S. ЛВ B в этих конструкциях определяет условие выполнения тела цикла.
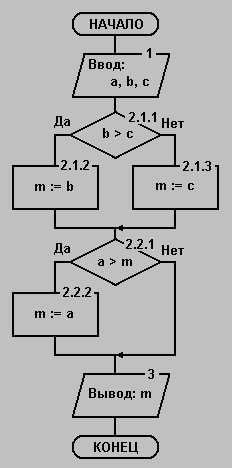
Рассмотрим пример разработки программы с применением метода пошаговой детализации. Задача: Составить программу определения максимального из трёх чисел входа. Сразу же можно предложить следующую абстрактную программу решения поставленной задачи:
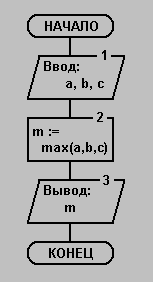
Эта программа содержит абстрактную операцию max(a,b,c). В этой связи выполним следующую детализацию блока 2:
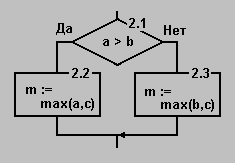
Очевидно, что блоки 2.2 и 2.3 нуждается в дальнейшей детализации:
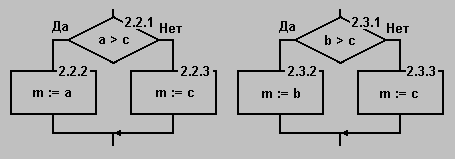
Теперь ни один из блоков не содержит абстрактных понятий и мы можем окончательно записать программу на базовом языке программирования:
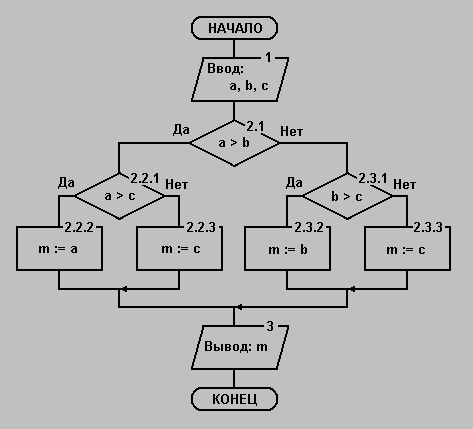
Интересно, что существует и другой вариант детализации блока 2:
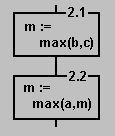
После детализации блоков 2.1 и 2.2 нового варианта детализации блока 2 и соответствующей сборки мы получим ещё один вариант программы:
Теперь мы имеем два варианта программы и, естественно, возникает задача выбора лучшей. Вторая программа содержит на два блока меньше и есть все основания считать, что она займёт меньше места в ОП. Зато первая программа будет работать в среднем быстрее. Для получения решения в первом варианте надо выполнить 5 блоков, а во втором в среднем 5.5. Выбор зависит от тех требований, которые предъявляются к программе. Это естественно, что за увеличение быстродействия программы приходится расплачиваться увеличением необходимой ей памяти.
В общем случае остаётся открытым вопрос о том как на каждом шаге процесса детализации выбирать нужную управляющую конструкцию. Здесь должна выручать интуиция программиста. На первых порах следует использовать метод проб и ошибок. Если на некотором шаге детализирующая конструкция была выбрана неправильно, то рано или поздно это станет ясно, и тогда надо вернуться назад и пересмотреть ранее принятое неправильное решение. Проделываемая при этом работа, как говорит Дейкстра - это расплата за отсутствие дара предвидения, который приходит вместе с опытом. В накоплении опыта программирования и состоит наша задача.
В абстрактной программе в логическом блоке может быть записано сложное логическое высказывание, для вычисления которого может потребоваться целый алгоритм. В ЯСА мы ограничимся теми рамками, которые предоставляет так называемое исчисление высказываний. Исчисление высказываний позволяет строить из простых высказываний (каковыми могут быть, например, арифметические сравнения) сложные с помощью трёх логических операций, а именно: НЕ (отрицание), И (конъюнкция) и ИЛИ (дизъюнкция) (обозначим их соответственно ~, & и | ).
Высказывание ~A истинно, если A ложно, и наоборот.
Высказывание A & B истинно, если истинны оба высказывания-операнда. Очевидно, что высказывание A & B будет ложным тогда, когда ложно одно из высказываний A или B.
Высказывание A | B истинно, если истинно хотя бы одно из высказываний-операндов. Очевидно, что высказывание A | B будет ложным только тогда, когда ложно A и ложно B.
На рис. 5 приведены схемы реализации логических операций исчисления высказываний. В верхнем ряду расположены логические блоки со сложными высказываниями, а в нижнем ряду приведена их реализация на ЯСА. Пунктиром обозначены реализуемые абстрактные логические блоки.
Рис. 5. Реализация логических операций исчисления высказываний
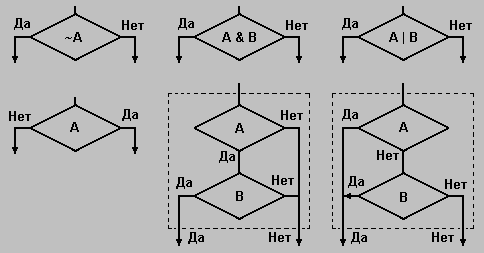
Начиная с этого момента мы введём в ЯСА новые три операции - ~, & и |. Действуя последовательно мы также должны предусмотреть круглые скобки для обозначения порядка выполнения логических операций в сложных высказываниях. Для сокращения числа скобок удобно ввести понятие приоритета операций, подобно тому, как это сделано в арифметике. По уменьшению приоритетов логические операции расположены так: ~, &, |. Аналогичным образом введём также логические переменные, логические константы ( 0 - "ложь", 1 - "истина") и логический оператор присваивания.
Совершенно очевидно, что введя в ЯСА-язык новые конструкции мы должны соответствующим образом усовершенствовать и ЯСА-машину.
Copyright г Барков Валерий Андреевич, 2000