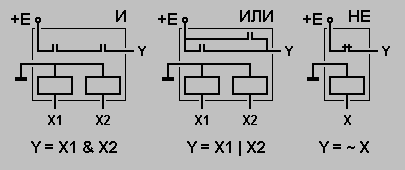
1. Булева алгебра
2. Логическая интерпретация
3. Функциональная интерпретация
4. Интерпретация на множествах
5. Интерпретация на переключательных
схемах
6. Программная модель многоразрядного
двоичного сумматора
Булева алгебра - это формальная система, состоящая из множества M={0,1} и операций ~ (отрицание), & (конъюнкция) и | (дизъюнкция).
Операции определим с помощью таблиц:
| A | ~A |
| 0 | 1 |
| 1 | 0 |
| A | B | A | B | A & B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Отметим, что операции ~, & и | отображают элементы множества M на само это множество.
Используя переменные, булевские операции и круглые скобки, можно строить булевские выражения. Например: A & ( B | ~A ) & ~B. При отсутствии скобок порядок выполнения операций определяется их приоритетами (по убыванию - ~, &, | ).
Для булевой алгебры справедливы следующие законы:
1. Закон коммутативности дизъюнкции: A | B = B | A .
2. Закон коммутативности конъюнкции: A & B = B & A .
3. Закон ассоциативности дизъюнкции: A | (B | C) = (A | B) |
C .
4. Закон ассоциативности конъюнкции: A & (B & C) =
(A & B) & C .
5. Закон дистрибутивности дизъюнкции
относительно конъюнкции: A | (B & C) = (A | B) & (A | C) .
6. Закон дистрибутивности конъюнкции
относительно дизъюнкции: A & (B | C) = (A & B) | (A & C)
.
7. Первый закон поглощения: A | (A & B) = A .
8. Второй закон поглощения: A & (A | B) = A .
9. Первый закон де Моргана: ~(A | B) = ~A & ~B .
10. Второй закон де Моргана: ~(A & B) = ~A | ~B .
11. Закон идемпотентности дизъюнкции: A | A = A .
12. Закон идемпотентности конъюнкции: A & A = A .
13. Закон снятия двойного отрицания: ~~A = A .
14. Первый закон отбрасывания: A | (B & ~B) = A .
15. Второй закон отбрасывания: A & (B | ~B) = A .
Здесь под A и B понимаются любые булевские выражения.
Кроме того непосредственно с помощью таблиц
можно убедиться в том, что
A | 0 = A, A | 1 = 1, A & 0 = 0, A & 1 = A.
В АЯ Pascal булева алгебра представлена типом Boolean, булевскими константами False и True, а также булевскими операциями not, and и or.
В качестве примера работы с булевскими операциями составим программу для экспериментальной проверки первого закона де Моргана.
program Morgan1;
var A,B: Boolean;
begin
for A:=False to True do
for B:=False to True do
if (not(A or B)) <> (not A and not B) then
begin
WriteLn('Morgan is liar.');
Exit;
end;
WriteLn('Morgan is right!');
end.
Если наша машина исправна и в программе нет ошибок, то на выходе мы должны получить:
Morgan is right!
Логическая интерпретация булевой алгебры позволяет использовать её аппарат для работы с логическими высказываниями. Логические значения "ложь" и "истина" соответствуют булевским 0 и 1. Логические связки НЕ, И, ИЛИ интерпретируются как операции ~, & и |, соответственно. Таблицы, которые мы использовали для определения булевских операций, в логике интерпретируются как таблицы истинности.
В практике исчисления высказываний принято оперировать также дополнительными связками, которые, впрочем, выражаются через булевские:
Название |
Обозначение | Определение |
| Импликация | A->B | ~A | B |
| Эквивалентность | A=B | ~A & ~B | A & B |
| Строгая дизъюнкция | A<>B | A & ~B | ~A & B |
Высказывания, которые истинны при всех возможных значениях входящих в них переменных, называются тождественно истинными (универсально общезначимыми, тавтологичными). Примеры: A | ~A, ~(A | B) = ~A & ~B .
Высказывания, которые ложны при всех возможных значениях входящих в них переменных, называются тождественно ложными (противоречиями). Пример: A & ~A .
В языке Pascal булева алгебра по-существу представлена в логической интерпретации. Для представления дополнительных связок можно использовать операции сравнения. Учитывая, что False < True, то в этой связи некоторые операции сравнения автоматически приобретают смысл логических связок: <= (импликация), = (эквивалентность), <> (строгая дизъюнкция).
y = f(x1) - 4 функции,
y = f(x1, x2) - 16 функций. Здесь x1, x2 и y - принадлежат M. В
общем случае
y = f(x1, x2, ..., xn) - 2^(2^n) функций.
Функция вида [~]x1 & [~]x2 & ... & [~]xn называется элементарной конъюнкцией. Она принимает значение 1 только на одном наборе значений аргументов. Для построения нужной функции достаточно построить дизъюнктивную форму из элементарных конъюнкций для тех наборов аргументов, на которых функция принимает значение 1. Такая форма называется дизъюнктивной нормальной формой (ДНФ).
В качестве примера построим функции для реализации одноразрядного двоичного сумматора: A, B - операнды, Ci - вход переноса, S - сумма, Co - выход переноса.
| A | B | Ci | S | Co |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
S = A&B&C | A&~B&~Ci | ~A&B&~Ci | ~A&~B&Ci,
Co = A&B | A&Ci | B&Ci.
В АЯ Pascal есть возможность определять булевы функции, которые зависят от булевых аргументов.
1 - универсальное множество,
0 - пустое множество,
~A - дополнение множества A до 1,
A & B - пересечение множеств A и B,
A | B - объединение множеств A и B.
Для определения смысла операций рассмотрим пример. Предположим, что есть список группы студентов: 1) Вася, 2) Коля, 3) Лена, 4) Петя, 5) Оля. Далее для краткости мы будем обозначать их номерами из списка.
Универсальное множество в данном случае это множество всех студентов: [1, 2, 3, 4, 5].
Пустое множество: [].
Далее пусть A это множество студентов знающих язык Pascal. Предположим, что A = [1, 3, 4, 5]. A B - это множество студентов знающих язык C++. Предположим, что B = [1, 2, 3].
При сделанных предположениях ~A = [2] и ~B = [4, 5] - множества студентов, которые не знают Pascal и C++, соответственно. Таковы в данном случае дополнения множеств A и B до универсального множества.
A & B = [1, 3] - это множество, в которое входят элементы, входящие одновременно в оба множества-операнда операции пересечения. Очевидно, что в данном случае это множество студентов, владеющих обоими языками.
A | B = [1, 2, 3, 4, 5] - это множество, в которое входят элементы, входящие в любое из множеств-операндов операции объединения. В данном случае это множество студентов, владеющих хотя бы одним языком.
Убедимся в справедливости второго закона де Моргана ~(A & B) = ~A | ~B для множеств примера. С учетом ранее полученных результатов, ~(A & B) = ~ [1,3] = [2, 4, 5] и ~A | ~B = [2] | [4, 5] = [2, 4, 5] . Итак, для данного случая закон верен.
В АЯ Pascal предусмотрены средства для работы со множествами, но об этом мы поговорим позже.
Реле. Переключательные схемы И, ИЛИ, НЕ.
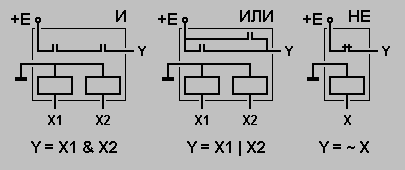
На основе переключательных схем можно построить одноразрядный двоичный сумматор S1.
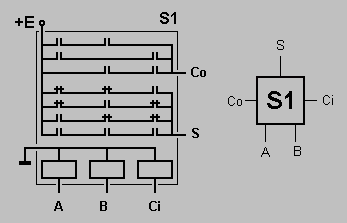
На основе одноразрядного двоичного сумматора можно построить многоразрядный двоичный сумматор.
В десятичной системе счисления: 137 = 10^2 * 1 + 10^1 * 3 + 10^0 * 7.
Аналогично в двоичной системе счисления:
5 -> 0101, так как 5 = 2^3 * 0 + 2^2 * 1
+ 2^1 * 0 + 2^0 * 1 и
6 -> 0110, так как 6 = 2^3 * 0 + 2^2 * 1
+ 2^1 * 1 + 2^0 * 0.
0101 + 0110 = ?
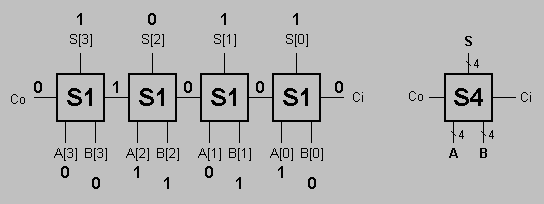
1011 -> 2^3 * 1 + 2^2 * 0 * 2^1 * 1 + 2^0 * 1 = 11
Таким образом задача построения устройств ЦВМ тоже решается на основе булевой алгебры.
В заключение составим программную модель многоразрядного двоичного сумматора, используя для выражения понятия логический элемент понятие подпрограммы.
program TstSm4;
const m = 4; {Количествово разрядов сумматора}
type TNumber = array[0..m-1] of Boolean;
var A,B,S: TNumber;
Co: Boolean;
procedure WrNumber(A: TNumber);
var i: Integer;
begin for i:=m-1 downto 0 do Write(Ord(A[i]):2) end;
procedure RdNumber(var A: TNumber);
var i,r: Integer;
begin
for i:=m-1 downto 0 do
begin Read(r); A[i]:=r=1 end
end;
procedure S1(A,B,Ci: Boolean; var S,Co: Boolean);
begin
Co := A and B or A and Ci or B and Ci;
S := A and B and Ci or
A and not B and not Ci or
not A and B and not Ci or
not A and not B and Ci;
end; {S1}
procedure Sm(A,B: TNumber; Ci: Boolean; var S: TNumber; var Co: Boolean);
var i: Integer; p,q: Boolean;
begin
q:=Ci;
for i:=0 to m-1 do
begin
S1(A[i],B[i],q,S[i],p);
q:=p;
end;
Co:=p;
end; {Sm}
begin
Write('A: '); RdNumber(A);
Write('B: '); RdNumber(B);
Sm(A,B,False,S,Co);
Write('A = '); WrNumber(A); WriteLn;
Write('B = '); WrNumber(B); WriteLn;
Write('S = ',Ord(Co):2); WrNumber(S); WriteLn;
end.
Пример выхода программы TstSm:
A: 0 1 0 1 B: 0 1 1 0 A = 0 1 0 1 B = 0 1 1 0 S = 0 1 0 1 1
Подобные программы применяются для логической отладки принципиальных электрических схем логических устройств ЦВМ.
Copyright г Барков Валерий Андреевич, 2000